At UIUC, I ended up taking a number of interesting courses that covered a range of topics, computational and theoretical tools and methods, that are helpful and insightful for generic as well as specific topics in computational physics. My take on some of these courses, the coursework involved as well as some other recommendations are given below:
Fast Algorithms and Integral Equation Methods (CS598APK): Prof Andreas Kloeckner
This course teaches a unique flavour of techniques and tools (including the famed Fast Multipole Method) for solving PDE boundary value problems, particularly in the integral equations formulation, where a significant reduction in the algorithmic cost can be achieved for problems that show super-linear runtime scaling. As a course project, I implemented a 2D Helmholtz PDE solver based on Combined Field Integral Equation (CFIE) formulation for acoustic scattering from a surface in a half-space domain with different boundaries conditions on the boundary wall. Shown below is a scattering phenomenon from a body (details in caption):
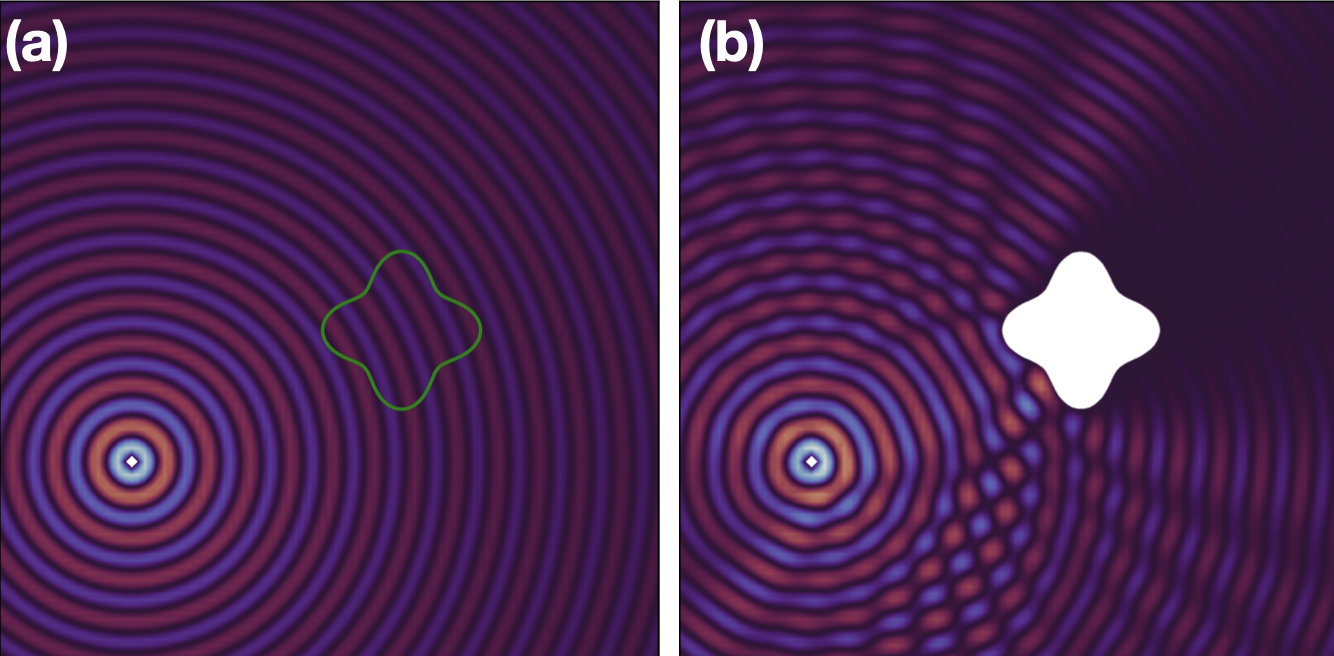
Numerical Methods for Partial Differential Equations (CS555): Prof Paul Fischer
This course builds a strong wide foundation of numerical analysis and computational physics by covering the basics of finite differences, volumes and elements (mostly), followed by advanced topics such as discontinuous Galerkin and spectral methods. As a course project, we solved the incompressible unsteady Navier–Stokes (UNS) equations using the spectral element method. Shown below is a result generated from our solver for a lid driven cavity (details in caption).
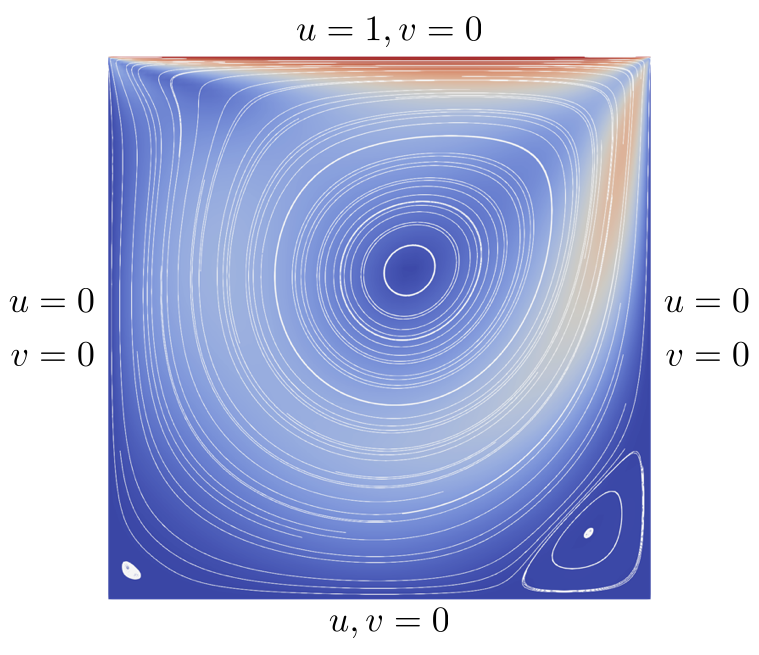
Theoretical courses
Besides the above numerical theme courses, I would also recommend (with my notes for reference) some theoretical courses offered at UIUC, that greatly enhance the understanding of physics and mechanics of the systems seen around us:
- Asymptotic Methods (TAM549): Prof Moshe Matalon
- Wave Motion (TAM518): Prof Sascha Hilgenfeldt